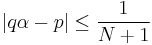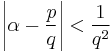Dirichlet's approximation theorem
In number theory, Dirichlet's theorem on Diophantine approximation, also called Dirichlet's approximation theorem, states that for any real number α and any positive integer N, there exists integers p and q such that 1 ≤ q ≤ N and
This is a foundational result in diophantine approximation, showing that any real number has a sequence of good rational approximations: in fact an immediate consequence is that for a given irrational α, the inequality
is satisfied by infinitely many integers p and q. This corollary also shows that the Thue–Siegel–Roth theorem, a result in the other direction, provides essentially the tightest possible bound, in the sense that the limits on rational approximation of algebraic numbers cannot be improved by lowering the exponent 2 + ε beyond 2.
Contents |
Method of proof
This theorem is a consequence of the pigeonhole principle. Dirichlet who proved the result used the same principle in other contexts (for example, the Pell equation) and by naming the principle (in German) popularized its use, though its status in textbook terms comes later.[1] The method extends to simultaneous approximation.[2]
See also
Notes
- ^ http://jeff560.tripod.com/p.html for a number of historical references.
- ^ Hazewinkel, Michiel, ed. (2001), "Dirichlet theorem", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=d/d032940
References
- Wolfgang M. Schmidt. Diophantine approximation. Lecture Notes in Mathematics 785. Springer. (1980 [1996 with minor corrections])
- Wolfgang M. Schmidt.Diophantine approximations and Diophantine equations, Lecture Notes in Mathematics, Springer Verlag 2000